Длина отрезка - это один из фундаментальных понятий геометрии, которое находит применение в различных областях математики и физики. Вычисление длины отрезка может быть необходимо при решении задач на плоскости или в пространстве, а также при построении геометрических фигур.
Существует несколько методов определения длины отрезка, в зависимости от известных данных и постановки задачи. Один из самых простых способов - использование координатной формулы вычисления расстояния между двумя точками на плоскости. Для этого необходимо знать координаты начала и конца отрезка и применить соответствующую формулу.
Кроме того, длину отрезка можно вычислить с помощью теоремы Пифагора, если известны длины трех сторон треугольника, одной из которых является искомый отрезок. Этот метод часто используется при работе с прямоугольными треугольниками.
Методы вычисления длины отрезка

Существует несколько способов вычисления длины отрезка между двумя точками в пространстве. Рассмотрим некоторые из них:
| 1. Формула расстояния между двумя точками в прямоугольной системе координат: | Если известны координаты точек A(x1, y1) и B(x2, y2), то длина отрезка AB равна: √((x2 - x1)^2 + (y2 - y1)^2) |
| 2. Использование теоремы Пифагора: | Если отрезок задан в виде прямоугольного треугольника со сторонами a, b, с гипотенузой c, то длина отрезка равна с = √(a^2 + b^2) |
| 3. Использование векторов: | Длина отрезка AB равна модулю вектора AB, то есть |AB| = √( (x2 - x1)^2 + (y2 - y1)^2 ) |
Формула длины отрезка

Длина отрезка AB = √((x₂ - x₁)² + (y₂ - y₁)²)
Где (x₁, y₁) и (x₂, y₂) - координаты начальной и конечной точек отрезка соответственно.
Геометрический метод измерения отрезка
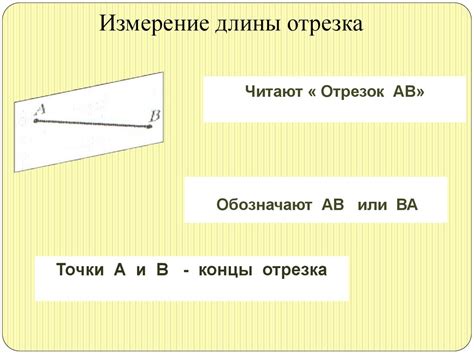
Для определения длины отрезка можно воспользоваться инструментами геометрии, такими как линейка, компас или другие геометрические инструменты. Нанесите отрезок на линейку или другой шкале, чтобы определить его длину в соответствии с единицами измерения.
Для измерения отрезка геометрическим методом также можно использовать пропорции и теоремы геометрии. Например, для измерения длины отрезка AB на плоскости можно воспользоваться теоремой Пифагора, если известны координаты точек A и B.
Использование координат для вычисления длины отрезка

Для вычисления длины отрезка по координатам его концов можно воспользоваться формулой расстояния между двумя точками на плоскости:
| Формула | Описание |
|---|---|
| Длина = √((x₂ - x₁)² + (y₂ - y₁)²) | где (x₁, y₁) и (x₂, y₂) - координаты концов отрезка |
Метод пифагоровых троек для определения длины отрезка

Для вычисления длины отрезка между точками A и B с координатами (x1, y1) и (x2, y2) соответственно, можно использовать следующий алгоритм:
| Шаг | Действие |
|---|---|
| 1 | Вычислить разность между x-координатами точек: dx = x2 - x1 |
| 2 | Вычислить разность между y-координатами точек: dy = y2 - y1 |
| 3 | Вычислить длину отрезка как квадратный корень из суммы квадратов разностей: length = sqrt(dx^2 + dy^2) |
Таким образом, метод пифагоровых троек позволяет эффективно вычислять длину отрезка, используя простые математические операции.
Применение тригонометрии для расчета длины отрезка

Для вычисления длины отрезка с помощью тригонометрии, можно воспользоваться формулой косинуса или синуса в прямоугольном треугольнике. Для этого необходимо знать длины двух сторон и угол между ними.
Пусть у нас есть отрезок AB, заданный координатами начальной точки (x1, y1) и конечной точки (x2, y2). Тогда длину отрезка можно вычислить по формуле:
| Длина AB = √((x2 - x1)² + (y2 - y1)²) |
Это основная формула для расчета длины отрезка с использованием тригонометрии. При этом, если угол между отрезком и осью x известен, можно применить формулу косинуса для определения длины отрезка:
| Длина AB = |x2 - x1| / cos(угол) |
Таким образом, подбор подходящего метода расчета длины отрезка с использованием тригонометрии зависит от доступной информации о точках и углах.
Алгоритмы программирования для вычисления длины отрезка

Для вычисления длины отрезка можно использовать различные алгоритмы программирования. Ниже рассмотрим несколько из них:
- По координатам точек: Для отрезка, заданного своими конечными точками A(x1, y1) и B(x2, y2), длина вычисляется по формуле: √((x2 - x1)² + (y2 - y1)²).
- С помощью теоремы Пифагора: Если отрезок задан координатами конечных точек в прямоугольной системе координат, то длину отрезка можно вычислить как гипотенузу прямоугольного треугольника, сторонами которого являются разности координат точек.
- Итеративный метод: Можно разбить отрезок на небольшие участки и вычислить их длину, затем сложить полученные значения.
- Использование векторов: Длина отрезка может быть найдена как модуль вектора, который задается координатами его конечных точек.
Интерполяционные методы определения длины отрезка

Интерполяционные методы позволяют вычислять длину отрезка с помощью аппроксимации кривой, которая задается набором точек на отрезке или его окрестности. Рассмотрим некоторые из них:
- Метод трапеций: данный метод представляет собой аппроксимацию графика функции на отрезке с помощью ломаной линии, состоящей из отрезков трапеции. Длина каждого отрезка вычисляется по формуле трапеции.
- Метод Симпсона: этот метод использует интерполяцию кубическими полиномами для приближения кривой на отрезке. Затем вычисляется интеграл от полученной функции, который дает длину отрезка.
- Использование сплайнов: сплайны позволяют аппроксимировать кривую на отрезке с использованием кусочно-полиномиальных функций. После этого можно вычислить длину кривой, которая будет приближенной длиной отрезка.
Использование интегралов для вычисления длины кривой
Для вычисления длины кривой используется метод интегрирования. Для этого необходимо знать параметризацию кривой, то есть уравнения, параметрически задающие положение каждой точки кривой.
Длина кривой может быть найдена с помощью определенного интеграла по длине кривой формулы:
L = ∫√(dx/dt)^2 + (dy/dt)^2 dt
где x(t) и y(t) - параметрические уравнения кривой, а t - переменная параметризации.
Интеграл рассчитывается на интервале, где t изменяется от начального значения до конечного, определяя длину кривой как результат интегрирования.
Сравнение различных методов расчета длины отрезка

Метод 1: Использование формулы расстояния между двумя точками
Для вычисления длины отрезка поэтому методу требуется знать координаты начальной и конечной точек отрезка. По формуле расстояния между двумя точками можно найти расстояние между этими точками и получить длину отрезка.
Метод 2: Применение теоремы Пифагора
Если отрезок задан прямоугольным треугольником, то длину отрезка можно найти путем применения теоремы Пифагора. По основным катетам треугольника можно найти гипотенузу, которая и будет являться длиной отрезка.
Метод 3: Использование векторов
Длину отрезка можно вычислить с использованием векторов. Разность координат соответствующих точек отрезка будет соответствовать направляющему вектору отрезка, а длина этого вектора будет равна длине отрезка.
Вопрос-ответ

Как можно вычислить длину отрезка без использования координат?
Длина отрезка может быть вычислена с помощью геометрических методов, например, используя формулу для расстояния между двумя точками на плоскости или в пространстве. Для этого необходимо знать координаты концов отрезка и применить соответствующую формулу, не прибегая к координатам.
Какие методы могут использоваться для определения длины отрезка?
Длину отрезка можно определить различными способами, например, используя геометрические формулы расстояния между точками, чертя отрезок по проиобразу в необходимой единице длины или измеряя его с помощью линейки или другого измерительного инструмента.