Геодезия – область науки, занимающаяся изучением формы Земли, ее размеров, плоскостей и углов на поверхности, а также разработкой методов и средств для определения географических координат точек на Земле.
Прямая геодезическая задача заключается в определении координат (географических или прямоугольных) новой точки на основе известных координат других точек и геодезических параметров (например, расстояний и азимутов).
Обратная геодезическая задача включает в себя определение расстояния и азимута между двумя точками на поверхности Земли на основе их географических координат.
Что такое геодезическая задача

Прямая геодезическая задача заключается в определении координат точек на поверхности Земли на основе наблюдений и измерений. Это включает определение широты, долготы, азимута, расстояния и других параметров.
Обратная геодезическая задача заключается в определении пути и положения объектов на Земле на основе известных координат. Это позволяет нам строить карты, планировать маршруты и выполнять другие задачи, связанные с географией и навигацией.
Понятие прямой геодезической задачи
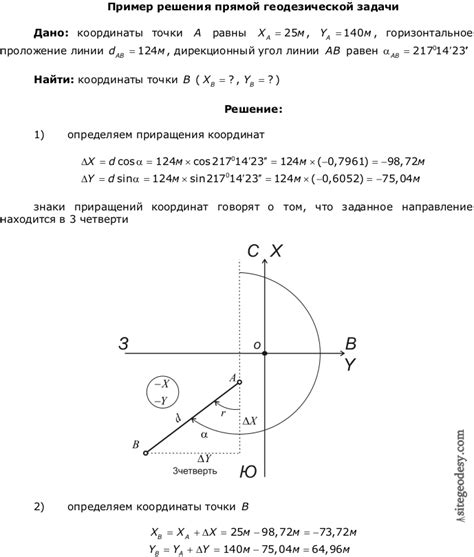
Прямая геодезическая задача в геодезии представляет собой задачу определения координат точки на Земле (или другой геодезической поверхности) по известным геодезическим параметрам. Она связана с определением расстояний, азимутов и других характеристик для заданных точек на поверхности Земли. Решение прямой геодезической задачи позволяет нам определить положение точки на поверхности по известным параметрам, таким как начальная точка, расстояние и азимут.
Для решения прямой геодезической задачи используются математические методы, такие как преобразование координат, геодезические формулы и алгоритмы.
| Примерные шаги для решения прямой геодезической задачи: |
| 1. Задать начальную точку и известные параметры (расстояние, азимут). |
| 2. Применить соответствующие геодезические формулы для расчета координат целевой точки. |
| 3. Получить координаты целевой точки на поверхности Земли. |
Понятие обратной геодезической задачи

Как решить геодезическую задачу

1. Определение известных параметров: Начните с определения всех известных параметров, таких как координаты начальной и конечной точек, направление и длина.
2. Выбор метода решения: Выберите подходящий метод для решения задачи, например, метод геодезических вычислений или метод прямой геодезической задачи.
3. Расчеты: Произведите необходимые расчеты, используя выбранный метод и учитывая все заданные параметры.
4. Проверка результатов: Проверьте полученные результаты на соответствие заданным условиям и корректность проведенных расчетов.
5. Интерпретация данных: Интерпретируйте полученные результаты, чтобы понять их значения и применение в конкретной задаче геодезии.
Примеры применения геодезической задачи

Геодезическая задача находит широкое применение в различных областях, включая:
| Отрасль | Примеры применения |
|---|---|
| Строительство | Разработка строительных проектов, планирование и мониторинг строительства зданий и сооружений |
| География | Создание карт, изучение топографических особенностей местности, планирование маршрутов |
| Навигация | Разработка геоинформационных систем, GPS-навигация, определение координат и расстояний |
| Геология | Исследование геологического строения земли, поиск полезных ископаемых, планирование рудников |
Эти примеры демонстрируют важность и разнообразие применения геодезической задачи в современном мире и ее влияние на различные области человеческой деятельности.
Вопрос-ответ

Что такое прямая геодезическая задача?
Прямая геодезическая задача в геодезии заключается в определении географических координат (широты и долготы) точки на Земле по известным параметрам, таким как расстояние, азимут и начальные координаты. Это задача нахождения местоположения точки по известным данным о направлении и расстоянии.
Что такое обратная геодезическая задача?
Обратная геодезическая задача в геодезии заключается в определении расстояния и азимута между двумя точками на поверхности Земли по их географическим координатам. Это задача нахождения расстояния и направления между двумя точками на основе их координат.
Какие ключевые понятия связаны с геодезическими задачами?
Для прямой и обратной геодезической задачи важны такие понятия, как географические координаты (широта и долгота), расстояние между точками на Земле, азимут (угол от севера) и геодезическая линия (кратчайшее расстояние между двумя точками на поверхности Земли).
Каким образом выполняется решение прямой и обратной геодезической задачи?
Для решения прямой и обратной геодезических задач используются специализированные методы и алгоритмы, основанные на геодезических формулах и математических моделях Земли. Для прямой задачи применяются формулы прямолинейной тригонометрии, а для обратной - методы обратной геодезии, позволяющие вычислить расстояние и азимут между точками по их координатам.



