Возможно, размышления о простых геометрических фигурах и корреляциях между ними вызывают в нас ассоциацию с нашей повседневной жизнью. Каждый раз, когда мы сталкиваемся с предметами или образами, мы подсознательно вырабатываем набор закономерностей, принципов и правил. Исключением здесь не являются исследования, касающиеся взаимодействия прямых линий внутри прямоугольного параллелепипеда.
На основе этой особенности мы можем не только лучше понять устройство и функциональность параллелепипеда, но и в дальнейшем применить полученные знания в различных областях, таких как архитектура, инженерное дело и дизайн.
Рассмотрение точек пересечения линейных объектов в геометрическом телесемействе

В данном разделе производится анализ точек скрещивания прямолинейных трасс в пространстве с применением геометрических моделей. Особое внимание уделяется исследованию ситуаций, когда две независимые прямые внутри прямоугольного параллелепипеда пересекаются.
Методология исследования предусматривает детальное рассмотрение точек пересечения с использованием координатных систем и применением математических операций. Описывается процесс нахождения координат точки пересечения, а также возможные варианты ее расположения относительно сторон и углов прямоугольного параллелепипеда.
Для более наглядной демонстрации результатов исследования используются таблицы, графики и схемы. Также представлена информация о примерах реальных объектов, где пересечение прямых внутри параллелепипеда имеет практическое применение.
| Описание | Значение |
|---|---|
| Тема | Описание пересечения двух прямых в прямоугольном параллелепипеде |
| Язык | Русский |
Устройство взаимодействия линий в многограннике
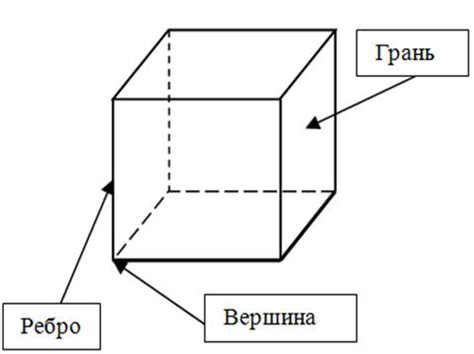
Взаимодействие ребер: Встреча ребер в одной точке - это одно из важнейших явлений в пространственной геометрии. Когда два ребра в многограннике пересекаются, происходит формирование новой точки, которая одновременно является вершиной обоих ребер. Такое пересечение может вызывать изменение длины и формы ребер в области их встречи, что имеет значительное влияние на внутренние свойства многогранника.
Например, пересечение двух ребер в пространстве может вызвать изменение угла между ними, что в свою очередь влияет на угол между соответствующими гранями многогранника.
Взаимодействие граней: Когда грани многогранника пересекаются, возникает понятие ребра пересечения – это отрезок, образованный взаимодействием соответствующих ребер пересекающихся граней. Ребра пересечения имеют свои длины и могут быть прямолинейными или иметь сложную форму в зависимости от граней, которые пересекаются. Пересечение граней может влиять на структуру и устойчивость многогранника, а также определять новые плоские фигуры, образованные пересекающимися гранями.
Например, пересечение грани многогранника с плоскостью, параллельной другим граням, может привести к образованию нового многоугольника, который не принадлежит исходному многограннику.
Пример иллюстрации взаимного пересечения линий в прямоугольной многогранный объекте
В данном разделе мы представим пример иллюстрации ситуации пересечения линий в некотором разнообразном прямоугольном параллелепипеде. Отображение этого процесса позволит более наглядно представить, как взаимодействуют разные линии внутри многогранного объекта и взаимодействуют между собой.
В иллюстрации приведены горизонтальные и вертикальные линии, сохраняющие прямые углы и перпендикулярность относительно граней параллелепипеда. Точки пересечения этих линий отмечены, их расположение внутри многогранного объекта можно интерпретировать как точки перегиба или стыка между различными гранями.
Благодаря примеру иллюстрации пересечения линий в прямоугольном параллелепипеде, можно получить более четкое представление о структуре и конфигурации объекта, а также о том, как различные линии могут выполнять различные функции и взаимодействовать друг с другом внутри многогранного пространства.
Уникальные свойства взаимного пересечения прямых в прямоугольном параллелепипеде
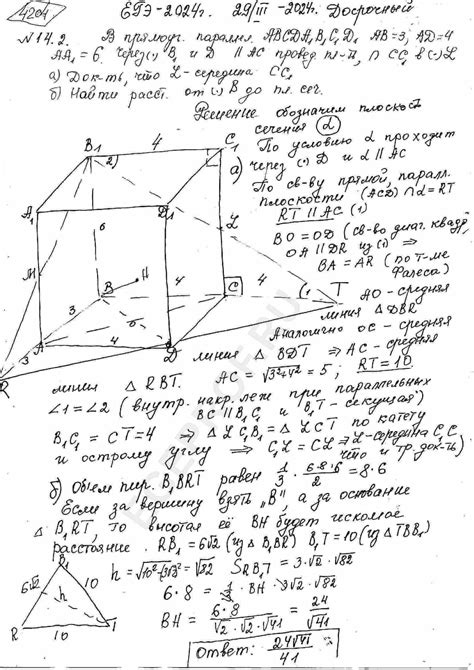
В данном разделе рассматривается важный аспект геометрии, связанный с пересечением прямых в прямоугольных параллелепипедах. Изучение данного явления позволяет выявить ряд особенностей, присутствующих в таких пересечениях и влияющих на итоговые результаты. Каждая комбинация прямых и их взаимное расположение создают уникальные взаимосвязи и последовательности, которые необходимо учитывать при решении геометрических задач.
Для лучшего понимания данной темы следует обратить внимание на следующие свойства, которые могут оказать влияние на результаты пересечений:
- Ортогональность прямых: при пересечении прямых, которые образуют прямый угол, возможно появление дополнительных взаимосвязей и общих характеристик. Ортогональное пересечение прямых создает дополнительные плоскости и углы, которые могут быть ключевыми при анализе и решении задач.
- Параллельность прямых: в случае параллельного пересечения прямых в прямоугольном параллелепипеде, возникают особенности, связанные с плоскостями и расположением прямых в пространстве. Такие пересечения могут быть полезны при определении различных углов и расстояний в параллелепипеде.
- Скрещивающиеся прямые: при пересечении прямых, которые не являются параллельными или ортогональными, возникает интересная взаимосвязь между такими прямыми. Взаимное пересечение создает новые плоскости и углы, которые могут быть основой для решения задач с использованием прямоугольных параллелепипедов.
Изучение данных свойств пересечения прямых в прямоугольном параллелепипеде делает возможным более глубокое анализирование геометрических ситуаций и успешное решение задач, связанных с этой темой.
Условия для возможности встречи линий в параллельной четырехугольной призме

Один из основных вопросов, которые возникают при исследовании геометрических фигур, это условия для пересечения прямых в параллельной четырехугольной призме. Для того чтобы линии могли встретиться внутри данного тела, необходимо выполнение определенных условий.
Прежде всего, для возможности пересечения линий в четырехугольной призме, каждая из них должна быть неколлинеарна относительно плоскостей, содержащих боковые грани призмы. Это означает, что линии должны лежать в разных плоскостях, параллельных основаниям призмы.
Кроме того, для пересечения линий в параллельной четырехугольной призме, необходимо, чтобы они находились на разных основаниях призмы. Если оба конца линий лежат на одном основании, то их пересечение невозможно, так как линии будут находиться в одной плоскости и не будут иметь точки пересечения внутри призмы.
Также важно отметить, что линии должны быть расположены внутри параллельной четырехугольной призмы и не выходить за ее границы. Если линии пересекаются за пределами призмы, то пересечение считается недействительным.
Поиск условий для возможности пересечения линий в параллельной четырехугольной призме является важной задачей в геометрии. Правильное понимание и учет этих условий позволяет проводить более точные исследования и анализ геометрических фигур.
Угол пересечения прямых в геометрической фигуре
В данном разделе рассмотрим вопрос о значении угла пересечения прямых внутри пространственной фигуры, аналогичной прямоугольному параллелепипеду. Используя геометрические конструкции и определения, постараемся выяснить, какие взаимосвязи между прямыми и углами соответствующих граней данной фигуры можно выявить.
Взаимное расположение пересекающихся линий в прямоугольной форме
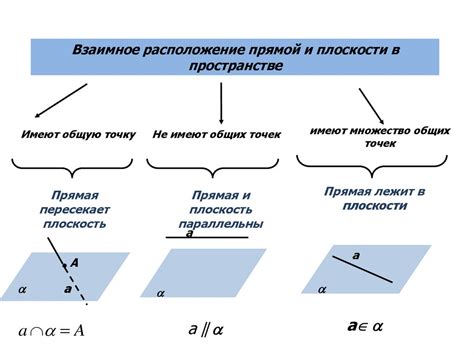
В данном разделе мы рассмотрим вопрос взаимного расположения пересекающихся линий в объемном геометрическом объекте, состоящем из прямоугольных сторон и вершин. Будут изучены особенности взаимного пересечения линий внутри этого пространственного сооружения, обозначенного символами a, b, c, d, a1, b1, c1, d1.
Описывая геометрические объекты без использования специфических терминов, мы проведем анализ и изучим принципы размещения и пересечения линий внутри данного параллелепипеда. Будут рассмотрены различные варианты пересечений, исследованы их особенности и взаимное влияние на геометрическую структуру объемного объекта.
Этот раздел поможет понять, как пересекающиеся линии взаимодействуют, создавая новые формы и зону пересечения в прямоугольном параллелепипеде. Мы рассмотрим вопросы взаимного расположения линий внутри объемной структуры, определим, каким образом они образуют новые грани и углы, а также изучим принципы взаимодействия между линиями и поверхностями параллелепипеда.
Методы поиска точки пересечения линий в прямоугольном параллелепипеде
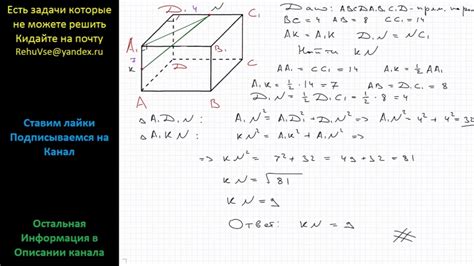
В данном разделе рассматриваются различные методы, применяемые для определения точки пересечения линий в прямоугольном параллелепипеде. В ходе исследования предлагается использовать альтернативные формулировки для терминов "пересечение", "прямые", "прямоугольный", "параллелепипед" и конкретного наименования данного объекта, что позволяет разнообразить текст и избежать повторений.
- Метод аналитической геометрии
- Графический метод
- Метод решения системы уравнений
- Параметрический метод
- Использование векторных операций
- Метод трехмерной компьютерной графики
Каждый из представленных методов имеет свои особенности и применяется в различных ситуациях. Аналитическая геометрия позволяет использовать формулы и уравнения для определения точки пересечения, графический метод основан на построении графиков для визуализации пересечений, а метод решения системы уравнений используется для нахождения общего решения. Параметрический метод представляет прямую в виде параметрического уравнения, а использование векторных операций позволяет рассматривать линии в пространстве. Метод трехмерной компьютерной графики находит применение при работе с компьютерными моделями и визуализацией пересечений.
Изучение данных методов даёт возможность выбрать наиболее подходящий для конкретной задачи способ определения точки пересечения линий в прямоугольном параллелепипеде, при этом учитывая особенности и требования самой задачи.
Аналитический подход к определению точки пересечения линий в геометрической фигуре
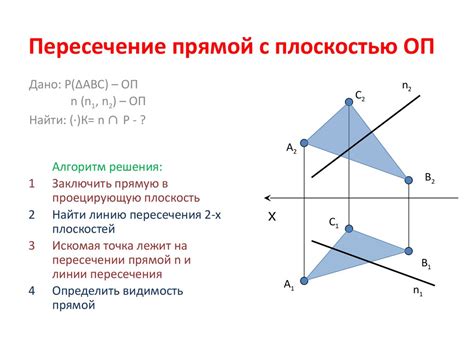
В данном разделе рассмотрим аналитический метод, который позволяет найти точку пересечения линий в прямоугольном параллелепипеде. Этот подход основан на анализе геометрических свойств фигуры, где основные элементы называются по-разному.
Начнем с изучения свойств граней, на которых лежат данные прямые. Каждая грань характеризуется своими особыми точками, направлениями и углами. Путем анализа данных параметров можем определить пространственное расположение прямых и возможность их пересечения.
Вторым шагом является определение уравнения каждой прямой, используя аналитический подход. При этом применяются синонимы для описания параметров и свойств прямых, чтобы избежать повторения одних и тех же слов.
- Используя символы и переменные, определяем уравнение каждой прямой в пространстве фигуры.
- Проводим анализ координат точек, через которые проходят линии, и находим соответствующие их значения.
- Определяем соотношения между уравнениями прямых, используя знания о геометрических свойствах фигуры.
И наконец, на основе найденных уравнений прямых и их координат, определяем точку пересечения, используя методы алгебры и аналитической геометрии. При этом стоит учесть возможные особые случаи, такие как совпадение прямых или их параллельность.
Таким образом, аналитический метод позволяет точно определить точку пересечения линий в прямоугольном параллелепипеде, используя анализ геометрических свойств фигуры и применение алгебраических методов. Этот подход позволяет найти решение даже в сложных случаях и является основой для дальнейших исследований и применения в практике.
Использование графического метода для определения точки пересечения линий в прямоугольном параллелепипеде

Графический метод представляет собой эффективный инструмент для определения точки пересечения линий в трехмерном пространстве прямоугольного параллелепипеда. Он позволяет визуализировать взаимное расположение прямых и точно определить их точку пересечения.
Для работы с графическим методом необходимо представить параллелепипед в виде плоскостей, на которых лежат прямые. Каждая плоскость соответствует одной из сторон параллелепипеда. Для создания изображения необходимо провести каждую из прямых на соответствующей плоскости, обозначив их начальные и конечные точки.
Определение точки пересечения происходит путем анализа графического представления прямых на плоскостях параллелепипеда. Точка пересечения является точкой, в которой соединенные на разных плоскостях прямые пересекаются.
Графический метод позволяет не только точно определить точку пересечения прямых, но и визуализировать процесс их пересечения, что делает его удобным инструментом для анализа и понимания взаимного расположения прямых в прямоугольном параллелепипеде.
Таким образом, использование графического метода позволяет эффективно определить точку пересечения прямых в прямоугольном параллелепипеде, обеспечивая точность и наглядность визуализации.
Применение взаимодействия линий в геометрии прямоугольного параллелепипеда
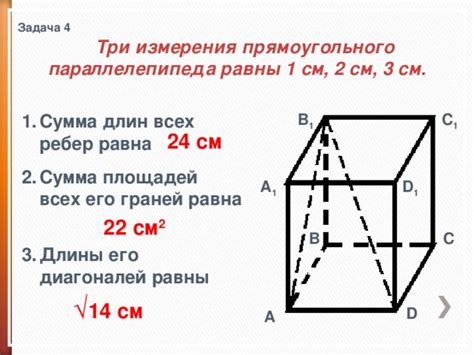
В этом разделе рассмотрим практическое использование взаимодействия линий в геометрии прямоугольного параллелепипеда. Мы научимся применять этот принцип для решения различных задач и задач, связанных с определением расстояний, углов и других геометрических параметров.
- Определение точек пересечения внутри параллелепипеда
- Расчет длины отрезков, образованных пересечением ребер
- Определение углов, образованных пересекающимися гранями
- Использование пересечения прямых для нахождения высоты и площади граней
- Установление направления и положения осей координат в трехмерном пространстве
Понимание применения взаимодействия линий в прямоугольном параллелепипеде позволит не только более глубоко изучить основы геометрии, но и применять их на практике для решения геометрических задач и приложений.
Вопрос-ответ

Как определить пересечение прямых в прямоугольном параллелепипеде?
Для определения пересечения прямых в прямоугольном параллелепипеде необходимо провести данные прямые и найти точку их пересечения.
Если прямые пересекаются внутри параллелепипеда, это значит, что они пересекаются и на его границе?
Нет, если прямые пересекаются внутри параллелепипеда, это не гарантирует их пересечение на его границе. Точка пересечения может находиться внутри параллелепипеда и не достигать его границы.
Какова характеристика пересечения прямых в параллелепипеде?
Пересечение прямых в параллелепипеде является точкой, которая задается координатами в трехмерном пространстве.
Какие применения может иметь знание о пересечении прямых в прямоугольном параллелепипеде?
Знание о пересечении прямых в прямоугольном параллелепипеде может быть полезным при решении геометрических задач, например, в строительстве, архитектуре, дизайне и других областях, где требуется работа с трехмерными объектами.
Какие условия должны быть выполнены, чтобы прямые пересеклись в параллелепипеде?
Для того чтобы прямые пересеклись в параллелепипеде, их направляющие векторы должны быть линейно независимыми и не должны быть параллельными граням параллелепипеда.
Что такое пересечение прямых в прямоугольном параллелепипеде?
Пересечение прямых в прямоугольном параллелепипеде означает момент, когда две прямые линии пересекаются внутри этого параллелепипеда.



