Понятие о параллельных прямых в геометрии известно каждому, кто сталкивался с основами математики. Однако вопрос о том, могут ли параллельные прямые пересечься в бесконечности, заставляет задуматься и вызывает интерес у тех, кто хочет глубже понять природу геометрических отношений.
Для того чтобы ответить на этот вопрос, необходимо разобраться в свойствах и особенностях параллельных прямых и понять, какие законы геометрии действуют в бесконечности. Параллельные прямые, по определению, никогда не пересекаются. Однако, в бесконечности геометрические правила могут меняться, что открывает новые возможности и предположения.
Исследование свойств параллельных прямых и их поведения в бесконечности - это увлекательный математический путь, который позволяет погрузиться в мир абстрактных концепций и выявить новые грани знаний о геометрии и алгебре.
Понятие параллельных прямых

Параллельные прямые обладают множеством свойств и являются важным понятием в геометрии. Например, у параллельных прямых углы, образуемые пересекающей прямой, равны между собой. Также параллельные прямые сохраняют свое расстояние и направление в любой точке их продолжения.
Определение геометрических объектов

- Точка – это абстрактное понятие, не имеющее размеров, обозначается буквой.
- Прямая – это бесконечное множество точек, лежащих на одной прямой, обозначается буквой или знаком.
- Отрезок – это участок прямой, ограниченный двумя точками, обозначается двумя конечными точками.
- Угол – это область плоскости, заключенная между двумя лучами, имеет величину.
- Параллельные прямые – это прямые, которые не пересекаются в плоскости.
Таким образом, геометрические объекты являются базовыми элементами для изучения пространственных отношений и форм в геометрии.
Аксиома Эвклида

Согласно аксиоме Эвклида, параллельные прямые никогда не пересекаются. Если они расположены в плоскости, то они будут бесконечно расстоянны друг от друга, и все их точки будут находиться на одинаковом расстоянии друг от друга на всей длине прямых.
Свойства параллельных прямых

Параллельные прямые никогда не пересекаются. Они лежат в одной плоскости и имеют одинаковый наклон, что делает их не имеющими точек пересечения. В случае, если две прямые параллельны, их расстояние между собой всегда постоянно, и отличается от расстояния между прямыми, которые не параллельны.
Свойства параллельных прямых:
- Параллельные прямые лежат в одной плоскости.
- У параллельных прямых одинаковый наклон и постоянное расстояние между ними.
- Параллельные прямые никогда не пересекаются.
Пересечение параллельных прямых

Параллельные прямые никогда не пересекаются. Они расположены таким образом, что все точки одной прямой находятся на одинаковом расстоянии от другой. Если мы утверждаем, что параллельные прямые пересекаются, то это противоречит самому определению параллельности.
Возможные варианты пересечения
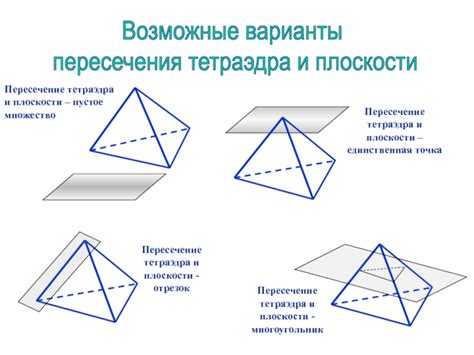
Параллельные прямые могут пересекаться в трех вариантах:
- Пересекаются в конечной точке:
- Пересекаются на бесконечности:
- Не пересекаются:
В этом случае прямые пересекаются в точке, которая находится за пределами бесконечности, но конечном расстоянии от начала координат.
Параллельные прямые могут пересекаться в бесконечности, когда направления прямых таковы, что они встречаются на бесконечности, а не в конечной точке.
Также существует ситуация, когда параллельные прямые не пересекаются в бесконечности и в конечной точке. Это происходит, когда угловой коэффициент исходных прямых совпадает, и прямые параллельны друг другу на протяжении всей прямой.
Альтернативные модели

Кроме классической геометрии Евклида, существует ряд альтернативных моделей, где аксиома о параллельных прямых может быть изменена. Например, в геометрии Римана, где пространство имеет неевклидову геометрию, параллельные прямые могут пересекаться в бесконечности. Это подтверждает, что строгость геометрических построений зависит от выбора аксиом и предположений.
Приведение к гиперболической геометрии

Чтобы понять, как параллельные прямые в гиперболической геометрии могут пересекаться в бесконечности, мы можем рассмотреть следующие преобразования: при сужении плоскости геометрического пространства, добавлении векторов и других операциях геометрических преобразований.
Гиперболическая геометрия вводит новые правила, которые отличаются от классической евклидовой геометрии. В этой геометрии параллельные прямые могут пересекаться в бесконечности, что делает ее интересной и уникальной.
Изучение гиперболической геометрии помогает расширить наше понимание пространства и могут применяться в различных областях математики и физики.
Завершение рассмотрения

На протяжении всего анализа мы выяснили, что параллельные прямые никогда не пересекаются. Даже если провести их до бесконечности, они будут оставаться параллельными и не встретятся. Это свойство геометрической системы, которое мы можем использовать во многих математических и инженерных задачах. Понимание этого принципа помогает нам лучше понять структуру прямых линий и их взаиморасположение. Параллельные прямые остаются параллельными даже в бесконечности, и это принцип лежит в основе многих математических теорем и задач.
Вопрос-ответ

Могут ли параллельные прямые пересечься в бесконечности?
Да, в проективной геометрии параллельные прямые расцениваются как пары прямых, пересекающихся в бесконечности. В этом контексте параллельные прямые всегда пересекаются в одной точке, которая находится в бесконечно удаленном направлении.
Как можно понять, что параллельные прямые пересекаются в бесконечности?
В геометрическом рассмотрении, когда говорят о пересечении параллельных прямых в бесконечности, имеют в виду их визуальное сближение при увеличении масштаба, что приводит к впечатлению их пересечения в точке, находящейся на бесконечном расстоянии.
Почему параллельные прямые считаются пересекающимися в бесконечности?
Идея пересечения параллельных прямых в бесконечности возникает из концепции проективной геометрии, где точка в бесконечности приводит к тому, что параллельные прямые имеют общую точку пересечения в бесконечности. Это удобное геометрическое средство, которое позволяет рассматривать параллельные прямые как специальный случай пересекающихся в бесконечности.
Каково значение пересечения параллельных прямых в бесконечности?
Понимание пересечения параллельных прямых в бесконечности важно для глубокого изучения геометрии и для работы с проективными преобразованиями. Это позволяет увидеть связь между прямыми и точками в бесконечности, открывая новые возможности для исследования геометрических объектов.